En la unidad anterior $3.4$ se explicó cómo resolver triángulos rectángulos de manera fundamental con las razones trigonométricas básicas, pero la trigonometría también emplea triángulos oblicuángulos para resolver problemas, siendo estos los triángulos que no tienen un ángulo recto en ninguno de sus tres ángulos y en consecuencia no se puede resolver por los mismos teoremas que se emplean en el triángulo rectángulo; como es el uso de teorema de Pitágoras o por las razones trigonométricas.
A razón de esto, los triángulos oblicuángulos se resuelven con teoremas llamados «ley de senos» y «ley de cosenos». En esta sección describiremos como resolver triángulos en general con el teorema del seno $o Ley del seno$, este teorema, es un resultado de la trigonometría que establece la relación de proporcionalidad existente entre las longitudes de lados de un triángulo cualquiera con los senos de sus ángulos interiores opuestos.
Introducción
Un triángulo oblicuángulo es aquel que no tiene un ángulo recto, con la finalidad de demostrar la ley de senos utilizaremos un triángulo oblicuángulo cualesquiera, iniciamos definiendo sus tres puntos $A, B, C$ con sus respectivos segmentos y se representan con letras minúsculas $$a, b, c$$ considerando la letra de su respectivo ángulo $$A, B, C$$ que están en lo opuesto.
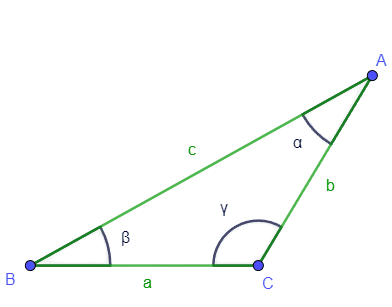
De forma que, en la siguiente figura, tenemos un triángulo oblicuángulo delimitado por los puntos ABC, cuyos ángulos son $\alpha$, $\lambda$ y $\varphi$, y sus lados opuestos correspondientes son BC, AB y AC ó también a, b y c.
Ley de los senos
Este teorema establece que dado un triángulo cualquiera oblicuo $sin ángulo recto$, con ángulos interiores $\alpha$, $\beta$ y $\gamma$ con lados opuestos de longitud $a$, $b$ y $c$. Entonces, se cumple la relación:
$$\dfrac{sin$\alpha$}{a} = \dfrac{sin$\beta$}{b} = \dfrac{sin$\gamma$}{c}$$
Pasos para aplicar la ley de los senos
Si se conoce la longitud de un lado y otras dos partes del triángulo, se pueden determinar las tres partes que restan empleando la ley de los senos, para ello se realizan los siguientes pasos:
- Se traza una línea perpendicular con dirección al ángulo opuesto, en nuestro caso es $A$, de esta amanera obtendremos dos triángulos rectángulos $ADC$ y $ADB$, como se muestra en la figura.
- La recta perpendicular con dirección al ángulo $A$, la denominamos con la letra $h$, esta recta es la altura del triángulo inicial $ABC$.
- Determinamos, en cada triángulo resultante, el seno de los otros dos ángulos: el seno del ángulo $B$ y del ángulo $C$, respectivamente, teniendo en común el segmento $\overline{AD}$, así como lo indica la figura. Recordando que:
$$\text{sen}\alpha = \dfrac{\text{cateto opuesto}}{\text{hipotenusa}}$$ - Calculamos el seno para el triángulo $ADC$, dados los valores:
$$ \triangle ADC = \begin{cases}
C & = \hphantom{-X} \text{ángulo} \\
b & = \hphantom{-X} \text{hipotenusa} \\
h & = \hphantom{-X} \text{altura, cateto opuesto} \\
CD & = \hphantom{-X} \text{cateto adyacente}
\end{cases}$$ $$\text{A partir del triángulo rectángulo anterior} ADC, \text{tenemos}: \text{sen}$C$ = \dfrac{h}{b}$$ $$\text{Despejamos la altura $h$ en cada razón, ya que es común en ambos triángulos}: b \cdot \text{sen}$C$ = h \Longrightarrow h = b \cdot \text{sen}$C$$$ - Procedemos igual para el segundo triángulo $ADB$, dados:
$$ \triangle ADB = \begin{cases}
B & = \hphantom{-X} \text{ángulo} \\
c & = \hphantom{-X} \text{hipotenusa} \\
h & = \hphantom{-X} \text{altura, cateto opuesto} \\
BD & = \hphantom{-X} \text{cateto adyacente}
\end{cases}$$ $$\text{A partir del triángulo rectángulo anterior} ADB: \text{sen}$B$ = \dfrac{h}{c}$$ $$\text{Despejamos la altura $h$ como en el caso anterior}: c \cdot \text{sen}$B$ = h \Longrightarrow h = c \cdot \text{sen}$B$$$ - Igualamos la altura $h$ obtenida para cada triángulo rectángulo: $$\begin{array}{cc} h = b\cdot \text{sen}$C$ & h = c\cdot \text{sen}$B$ \end{array}$$ $$\text{Como la altura es la misma para ambos triángulos rectángulos, establecemos una igualdad} :\; h =h $$ $$b\cdot \text{sen}$C$ = c\cdot \text{sen}$B$$$
- Despejando obtenemos cada ángulo y su cateto correspondiente, obteniendo una igualdad, la cual corresponde a la ley de senos de los dos triángulos rectángulos con respecto al ángulo $B$ y el ángulo $C$:
$$b\cdot \text{sen}$C$ = c\cdot \text{sen}$B$ \Longrightarrow \dfrac{\text{sen}$C$}{c} = \dfrac{\text{sen}$B$}{b} $$ - Luego, en el triángulo $ABC$, aplicando la altura desde el vértice $C$ hasta el lado $\overline{AB}$, de la misma forma que lo hicimos en los puntos anteriores, entonces:
$$\dfrac{\text{sen}$A$}{a} = \dfrac{\text{sen}$B$}{b}$$ - Al combinar $6$ y $7$ se llega al resultado esperado:
$$\dfrac{\text{sen}$A$}{a} = \dfrac{\text{sen}$B$}{b} = \dfrac{\text{sen}$C$}{c}$$
Tips para usar la Ley de los senos
Para aplicar el teorema o ley del seno se necesita que el triángulo sea oblicuángulo $que no tiene un ángulo recto$ y conocer los valores de 3 de 4 variables $siendo L = lado y A = ángulo$, como:
- LLA dos lados y un ángulo opuesto a uno de ellos.
- AAL dos ángulos y cualquier lado opuesto a uno de ellos.
- ALA dos ángulos y cualquier lado opuesto a uno de ellos.

Aplicándose acorde a lo anterior:
$$\begin{array}{ccc} \dfrac{sin$\alpha$}{a} \;=\; \dfrac{sin$\beta$}{b} \qquad & \qquad \dfrac{sin$\alpha$}{a} \;=\; \dfrac{sin$\gamma$}{c} \qquad & \qquad \dfrac{sin$\beta$}{b} \;=\; \dfrac{sin$\gamma$}{c} \end{array}$$
Déjanos un comentario No hay comentarios