En el vasto mundo de las matemáticas, las funciones trigonométricas recíprocas ocupan un lugar esencial al revelar las relaciones inversas de las funciones trigonométricas comunes. Estas funciones, también conocidas como funciones trigonométricas inversas o funciones arcotangentes, ofrecen un enfoque alternativo para resolver problemas y entender patrones en fenómenos naturales y científicos. En esta unidad, exploraremos en qué consisten las funciones trigonométricas recíprocas y cómo se aplican en diversas disciplinas.
¿Qué son las funciones trigonométricas recíprocas?
Las funciones trigonométricas recíprocas son el resultado de multiplicar las funciones trigonométricas tradicionales, como el seno, el coseno y la tangente por otra donde el resultado es igual a la unidad $1$. En otras palabras, en matemáticas, dos cantidades son recíprocas, si su producto es igual a uno. Por ejemplo:
$$\frac{2}{5}ㅤ\text{esㅤunㅤrecíprocoㅤa}ㅤ\frac{5}{2},ㅤ\text{porque:} \left$ \frac{2}{5} \right$x\left$ \frac{5}{2} \right$ = 1$$
De lo anterior se deduce que las funciones trigonométricas recíprocas son, dos funciones cuyo producto es igual a la unidad.
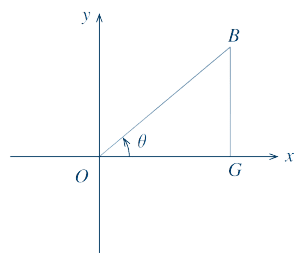
Partiendo de la siguiente gráfica, se tiene que las funciones trigonométricas para el triángulo OGB son:
$$senθ=\frac{\overline{\rm BG}}{\overline{\rm OB}}ㅤㅤcosθ=\frac{\overline{\rm OG}}{\overline{\rm OB}}$$
$$tanθ=\frac{\overline{\rm BG}}{\overline{\rm OG}}ㅤㅤcotθ=\frac{\overline{\rm OG}}{\overline{\rm BG}}$$
$$secθ=\frac{\overline{\rm OB}}{\overline{\rm OG}}ㅤㅤcscθ=\frac{\overline{\rm OB}}{\overline{\rm BG}}$$
Función recíproca del seno
Si multiplicamos $\text{sen}θ$ por $\cscθ$, tenemos:
$$$\text{sen}θ$.$\cscθ$ = \left$\frac{\overline{\rm B̵G̵}}{\overline{\rm OB}}\right$.\left$\frac{\overline{\rm OB}}{\overline{\rm BG}}\right$$$
Entonces:
$$$\text{sen}θ$.$\cscθ$ = 1$$
Despejando $\text{sen}θ$ en la función anterior, tenemos: $$\text{sen}θ = \frac{1}{\cscθ}$$
Y si despejamos para $\cscθ$, resulta: $$\cscθ=\frac{1}{\text{sen}θ}$$
∴ El seno es recíproco a la cosecante.
Función recíproca del coseno
Ahora, si multiplicamos $\cosθ$ por $\secθ$, tenemos:
$$$\cscθ$.$\secθ$=\left$ \frac{\overline{\rm OG}}{\overline{\rm OB}} \right$.\left$ \frac{\overline{\rm OB}}{\overline{\rm OG}} \right$$$
Luego, tenemos que:
$$$\cosθ$.$\secθ$=1$$
Despejando $\cosθ$, tenemos: $$\cosθ = \frac{1}{\secθ}$$
Y despejando para $\secθ$, queda: $$\secθ=\frac{1}{\cosθ}$$
∴ El coseno es recíproco de la secante.
Función recíproca de la tangente
Al multiplicar $\tanθ$ por $\cotθ$, tenemos:
$$$\tanθ$.$\cotθ$=\left$ \frac{\overline{\rm B̵G̵}}{\overline{\rm OG}} \right$.\left$ \frac{\overline{\rm OG}}{\overline{\rm BG}} \right$$$
De donde,
$$$\tanθ$.$\cotθ$=1$$
Despejando para $\tanθ$, tenemos: $$\tanθ= \frac{1}{\cotθ}$$
Y despejando para $\cotθ$, queda: $$\cotθ=\frac{1}{\tanθ}$$
∴ La tangente es recíproco de la cotangente.
Déjanos un comentario No hay comentarios