Resolver triángulos rectángulos utilizando razones trigonométricas implica encontrar las medidas desconocidas de los lados y ángulos de un triángulo rectángulo conocidos algunos de sus elementos. Las razones trigonométricas $seno, coseno y tangente$ se utilizan para relacionar los ángulos con las longitudes de los lados del triángulo. La expresión “resolver un triángulo” quiere decir que se desea determinar la longitud de cada lado y la medida de cada ángulo del triángulo. Se puede resolver cualquier triángulo rectángulo si se conocen dos lados o un ángulo agudo y un lado.
Pasos para resolver un triángulo rectángulo
Aquí tienes los pasos básicos para resolver un triángulo rectángulo mediante razones trigonométricas:
- Identifica el triángulo rectángulo: Asegúrate de que tienes un triángulo con un ángulo recto $90 grados$. Un triángulo rectángulo tiene un cateto opuesto al ángulo recto y un cateto adyacente al ángulo recto.
- Conoce los datos proporcionados: Realiza un esquema del triángulo e identifica los datos que conoces. Puede ser la longitud de uno o dos lados del triángulo y/o el valor de uno de los ángulos agudos.
- Decide qué quieres encontrar: Determina qué deseas calcular: ya sea un ángulo desconocido o la longitud de un lado desconocido.
- Aplica razones trigonométricas: Utiliza las razones trigonométricas que hemos estudiado hasta esta unidad, incluso las razones trigonométricas inversas o recíprocas. En función de lo que necesitas calcular como:
- Seno $sen$: Se define como el cateto opuesto dividido por la hipotenusa. $$\text{sen}θ = \frac{\text{cateto opuesto}}{\text{hipotenusa}}$$
- Coseno $cos$: Se define como el cateto adyacente dividido por la hipotenusa. $$\cos θ = \frac{\text{cateto adyacente}}{\text{hipotenusa}}$$
- Tangente $tan$: Se define como el cateto opuesto dividido por el cateto adyacente. $$\tan θ = \frac{\text{cateto opuesto}}{\text{cateto adyacente}}$$
- Realiza cálculos y resuelve: Dependiendo de los datos que conozcas y lo que quieras calcular, puedes utilizar las razones trigonométricas para resolver ecuaciones y encontrar las medidas desconocidas.
- Verifica tus resultados: Siempre verifica tus resultados para asegurarte de que sean coherentes con las propiedades trigonométricas y las restricciones del problema.
Recuerda que los triángulos rectángulos siguen el teorema de Pitágoras $$a^2 + b^2 = c^2$$, y las razones trigonométricas son relaciones entre los lados y los ángulos de estos triángulos. Practicar la resolución de varios ejemplos como los que tenemos a continuación, te ayudará a mejorar tus habilidades en la aplicación de razones trigonométricas para resolver triángulos rectángulos.
Como se verá en los ejemplos que siguen, una parte esencial del proceso de solución es trazar e identificar el triángulo. Luego, se explicará como hallar los lados y los ángulos de un triángulo rectángulo, si solamente se conocen algunos de ellos. En los siguientes dibujos, los lados y ángulos de color rojo son los que no se conocen, mientras los que son negros sí. Vamos a distinguir entre los siguientes casos, dependiendo de los elementos del triángulo que se conocen.
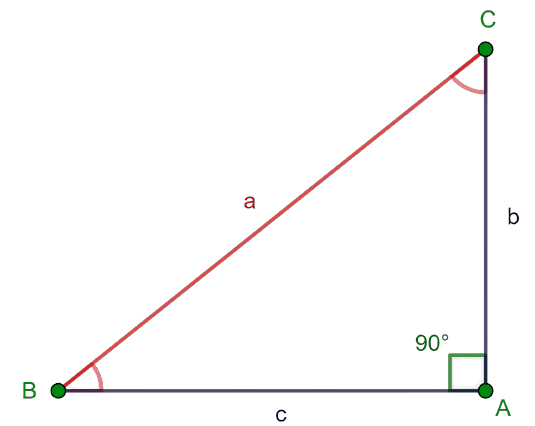
Se conocen dos catetos
En este caso se tiene que encontrar los dos ángulos agudos $$B$ y $C$$ y la hipotenusa $es decir, el lado $a$$.
- El ángulo $B$ es: $B = \tan\Big$ \dfrac{b}{c}\Big$$
- Los ángulos internos de cualquier triángulo suman $180^\circ $, por lo tanto $B + C = 90$, de donde el ángulo $C$ es: $C = 90^\circ – B$
- La hipotenusa es: $a = \dfrac{b}{\text{sen}$B$}$También se puede calcular mediante el Teorema de Pitágoras, con la igualdad: $a = \sqrt{b^2 + c^2}$
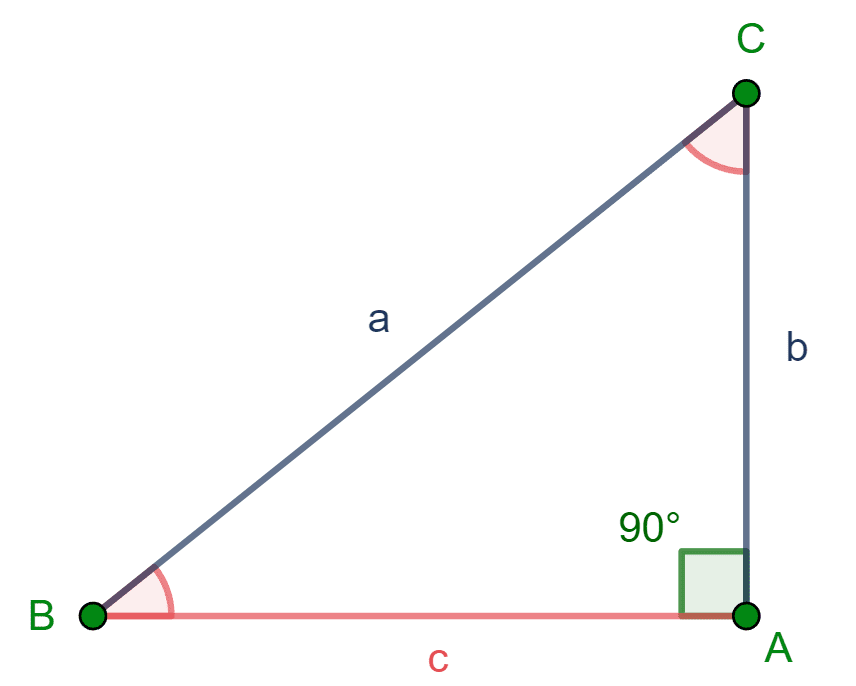
Se conocen la hipotenusa y un cateto
En este caso se deben encontrar los elementos en rojo, esto es, el cateto del lado $c$ y los dos ángulos agudos, es decir, los ángulos $B$ y $C$.
- El ángulo $B$ es: $B=\text{sen}\Big$ \dfrac{b}{a} \Big$$
- El ángulo $C$ es: $C=90^\circ -B$
- Dado que $\cos B = \Big$ \dfrac{c}{a}\Big$$ , entonces, el lado $c$ es: $c = a\cdot \cos$B$$
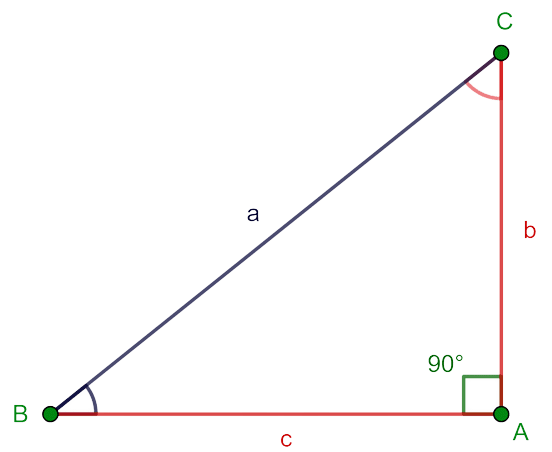
Se conocen la hipotenusa y un ángulo agudo
En este caso se deberá hallar el otro ángulo agudo $es decir, $C$$ y los dos catetos $$b$ y $c$$.
- El ángulo $C$ es: $C=90^\circ -B$
- El lado $b$ es: $b = a\cdot\text{sen}$B$$
- El lado $c$ es: $c = a\cos$B$$. También se puede calcular haciendo: $c = \sqrt{a^2+b^2}$
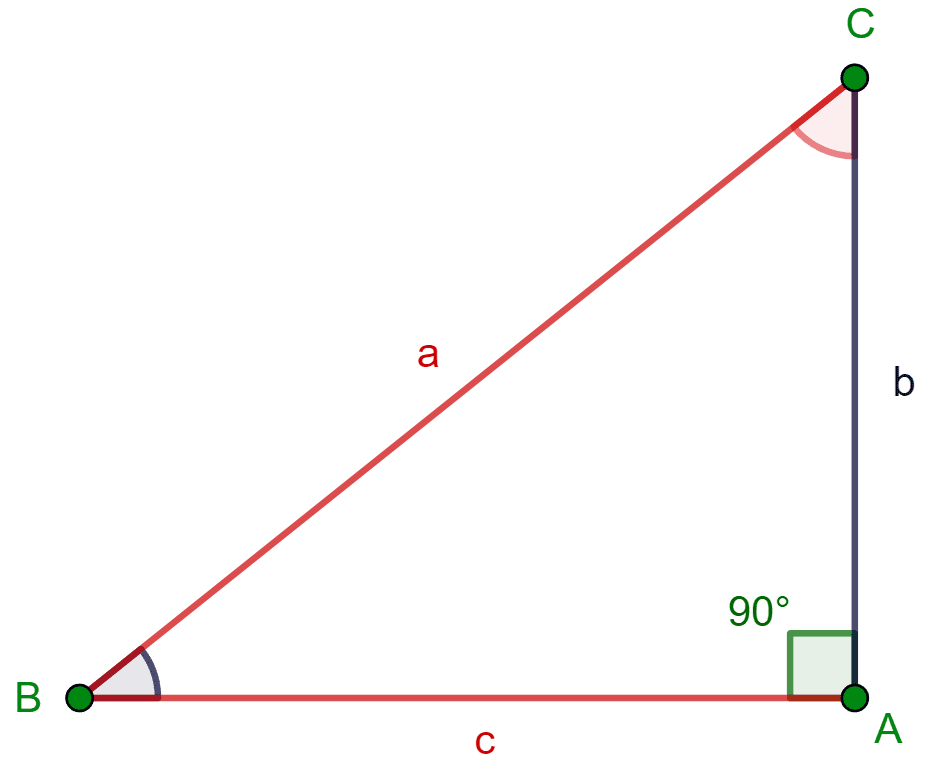
Se conocen un cateto y un ángulo agudo:
Aquí se deberá calcular el otro ángulo agudo $como antes, $C$$, la hipotenusa $el lado $a$$ y el otro cateto $el lado $c$$.
- El ángulo $C$ es: $C=90^\circ – B$
- El lado $a$ es: $a = \dfrac{b}{\text{sen}$B$}$
- El lado $c$ es: $c = \dfrac{b}{\tan$B$}$. También: $c = \sqrt{a^2+b^2}$
Déjanos un comentario No hay comentarios