1.1 Área bajo la curva
1.1.1 Introducción
Sabemos determinar áreas de figuras geométricas regulares, como son:
Cuyas áreas las determinamos como:
$$A_{T} = \frac{(base)(altura)}{2}$$
$$A_{Cu} = (lado)(lado)$$
$$A_{R} = (base)(altura)$$
$$A_{Ci} = \pi(radio)^2$$
Ahora, ¿Cómo determinamos el área de figuras irregulares?, como las mostradas a continuación:
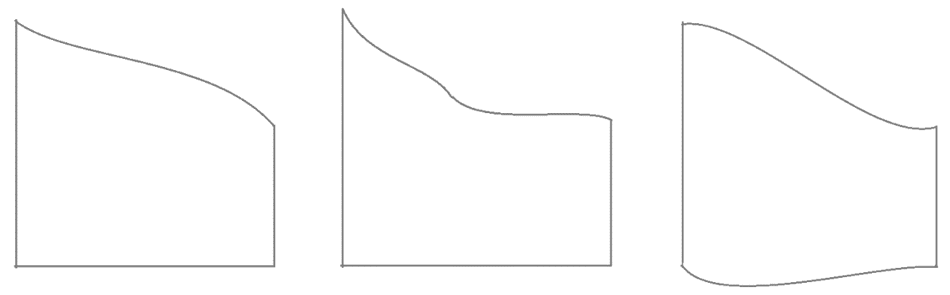
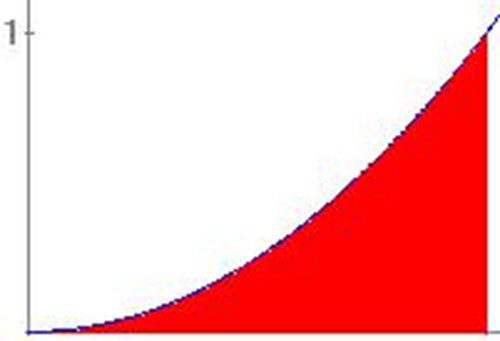
Para determinar el área de estas figuras no es posible separar en triángulos, ya que cuentan con un lado curvo. Así que, para determinar su área, empecemos considerando que la curva es una función, que está definida en el intervalo \([a,b]\), como se muestra en la siguiente figura:
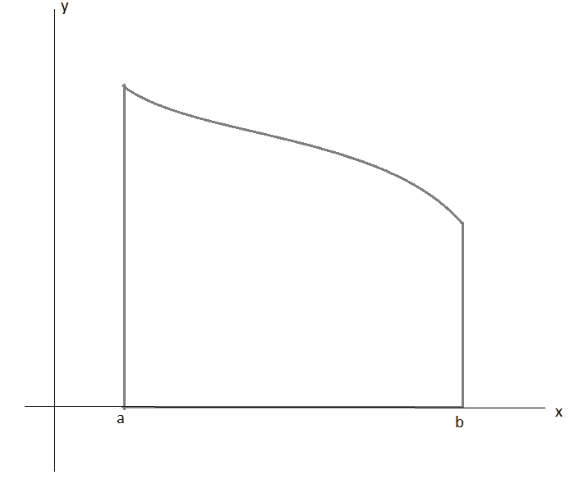
Seguido de esto, dividiremos la función en rectángulos, como se observa en la siguiente figura:
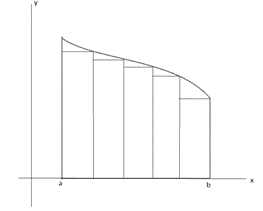
Si determinamos el área de cada rectángulo y las sumamos nos aproximaremos al área de la figura.
Ejemplo 1. Estimemos el área de una región \(R\) en particular, que se encuentra acotada por la gráfica de \(f(x) = x^2\), el eje \(x\) y la recta \(x = 1\), como se muestra en la figura 5.
Primero, tenemos que el área será un valor entre 0 y 1 por que \(R\) está contenida en un cuadrado de longitud \(1\).
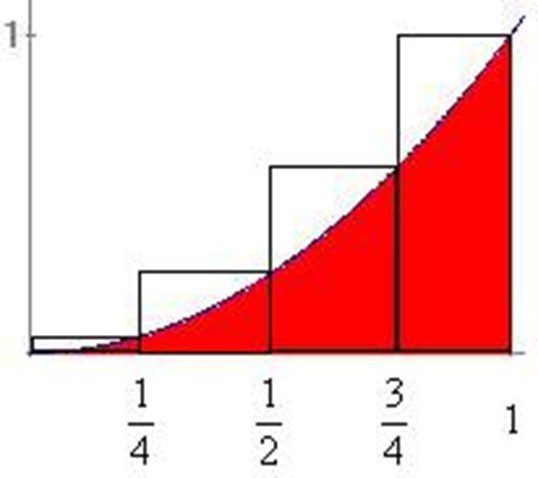
Para dar una aproximación dividamos la región en 4 rectángulos de igual longitud. Posteriormente, obtengamos el área de los rectángulos y sumémoslas. La base de cada rectángulo tiene el mismo valor porque las divisiones son iguales, es decir \(base=\frac{1}{4}\), y para la altura de los rectángulos tomemos el lado derecho del rectángulo, nos damos cuenta de que está representada por la función evaluada en el valor de la abscisa \(f(x) = x^2\), por lo tanto, \(altura=f(x)\) (Figura 6).
$$A_{R_{n}} = (base)(altura)$$ $$A_{R_{1}} = \frac{1}{4}f\left( \frac{1}{4} \right) = \frac{1}{4}\left( \frac{1}{4} \right)^2 = \frac{1}{4}\left( \frac{1}{16} \right) = \frac{1}{64}$$ $$A_{R_{2}} = \frac{1}{4}f\left( \frac{1}{2} \right) = \frac{1}{4}\left( \frac{1}{2} \right)^2 = \frac{1}{4}\left( \frac{1}{4} \right) = \frac{1}{16}$$ $$A_{R_{3}} = \frac{1}{4}f\left( \frac{3}{4} \right) = \frac{1}{4}\left( \frac{3}{4} \right)^2 = \frac{1}{4}\left( \frac{9}{16} \right) = \frac{9}{64}$$ $$A_{R_{4}} = \frac{1}{4}f(1) = \frac{1}{4}(1)^2 = \frac{1}{4}(1) = \frac{1}{4}$$ $$A_{R_{C}} = \frac{1}{64}+\frac{1}{16}+\frac{9}{64}+\frac{1}{4}=\frac{1}{64}+\frac{4}{64}+\frac{9}{64}+\frac{16}{64}=\frac{30}{64}\approx 0.46875$$ $$R \lt A_{R_{C}}$$
Si en lugar de considerar como la altura el punto extremo derecho, se considera el punto extremo de la izquierda del rectángulo, se tendría lo siguiente.
$$A_{R_{1}} = \frac{1}{4}(0)^2 = 0$$ $$A_{R_{2}} = \frac{1}{4}\left( \frac{1}{4} \right)^2 = \frac{1}{64}$$ $$A_{R_{3}} = \frac{1}{4}\left( \frac{1}{2} \right)^2 = \frac{1}{16} = \frac{4}{64}$$ $$A_{R_{4}} = \frac{1}{4}\left( \frac{3}{4} \right)^2 = \frac{9}{64}$$ $$A_{R_{I}} = 0 + \frac{1}{64} + \frac{4}{64} + \frac{9}{64} = \frac{14}{64} = \frac{7}{32} \approx 0.21875$$ $$A_{R_{I}} \lt R \lt A_{R_{C}}$$
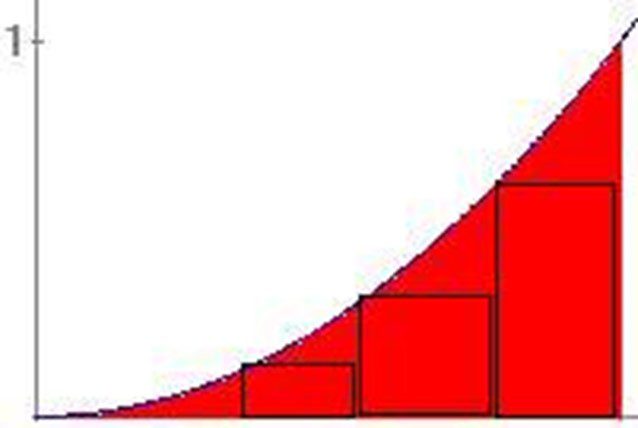
Es importante observar que, en este caso, la función es creciente y positiva, de tal forma que:
– Si consideramos los puntos extremos del lado derecho de los rectángulos, estos son circunscritos o también llamados por exceso.
– Si consideramos los puntos extremos del lado izquierdo de los rectángulos, estos están inscritos llamados por defecto.
Por lo tanto, el área de la región \(R\) se encuentra entre los dos siguientes valores: $$0.21875 \lt R \lt 0.46575$$
Podemos repetir este procedimiento con un número mayor de rectángulos, por ejemplo con 8.
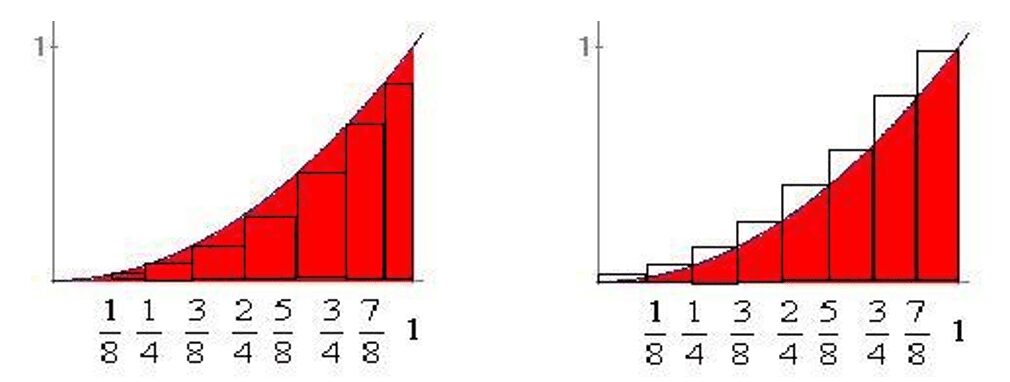
Se obtendría una mejor estimación para el área de la región \(R_{8}\). Al realizar el mismo proceso que hicimos para cuatro rectángulos, pero ahora para 8, obtenemos los siguientes valores: $$0.2734375 \lt R \lt 0.3984375$$ Podemos concluir entonces, cuanto más grande sea n (número de divisiones/rectángulos) mejor es la aproximación del área.
Notación de la Sumatoria
Es importante hacer un breve recorrido por las propiedades de las sumatorias y revisar algunas de ellas, ya que serán empleadas como parte del proceso de la obtención de áreas bajo la curva.
Sea n un entero positivo y sean \(a_{1}, a_{2}, …, a_{n}\) dos conjuntos de números reales. Entonces: $$i.\sum_{k=1}^n c = nc$$ $$ii.\sum_{k=1}^n (a_{k} + b_{k}) = \sum_{k=1}^na_{k} + \sum_{k=1}^nb_{k}$$ $$iii.\sum_{k=1}^n Ca_{k} = C\sum_{k=1}^na_{k}\:\:\:\forall \:\:número\:\:real\:\:C$$ $$iv.\sum_{k=1}^n (a_{k} – b_{k}) = \sum_{k=1}^na_{k} – \sum_{k=1}^nb_{k}$$
$$1.\:\:\sum_{k=1}^nk = 1+2+3+…+n=\frac{n(n+1)}{2}$$ $$2.\:\:\sum_{k=1}^nk^2 = 1^2+2^2+3^2+…+n^2=\frac{n(n+1)(2n+1)}{6}$$ $$3.\:\:\sum_{k=1}^nk^3 = 1^3+2^3+3^3+…+n^3=\left( \frac{n(n+1)}{2} \right)^2$$ $$4.\:\:\sum_{k=1}^nk^4 = 1^4+2^4+3^4+…+n^4=\frac{n(n+1)(2n+1)(3n^2+3n-1)}{30}$$ $$5.\:\:\sum_{k=1}^nk^5 = 1^5+2^5+3^5+…+n^5=\frac{n^2(n+1)^2(2n^2+2n-1)}{12}$$