La trigonometría, como la palabra lo indica, se refiere a la medida de los lados y los ángulos de un triángulo. La trigonometría plana se limita a triángulos que se encuentran en un plano y se basa en ciertas relaciones, llamadas funciones trigonométricas, que se definen más adelante. Por lo que comenzamos nuestro estudio de la trigonometría con la descripción de los ángulos y dos métodos para medirlos: en grados y en radianes.
Como veremos luego, la medida de un ángulo en radianes es lo que nos permite definir funciones trigonométricas en conjuntos de números reales. Estas funciones desempeñan también un importante papel en el estudio de toda clase de fenómenos vibratorios: sonido, luz, electricidad, etc. En consecuencia, una porción considerable de este curso se refiere al estudio de las propiedades y relaciones entre las funciones trigonométricas.
Ángulos
En trigonometría con frecuencia interpretamos a los ángulos como rotaciones de rayos. Así, un ángulo se forma con dos rayos o semirrectas, que tienen un extremo común llamado vértice. A un rayo lo llamaremos lado inicial $l_1$ del ángulo, y al otro, lado terminal $l_2$. Es útil imaginar al ángulo como formado por una rotación, desde el lado inicial hasta el lado terminal, como se ve en la figura. El ángulo se puede poner en un plano cartesiano con su vértice en el origen y su lado inicial que coincida con el eje positivo de las x, en ese caso se dice que el ángulo está en su posición normal o estándar.
La cantidad o dirección de rotación no está restringida en ninguna forma, si introducimos un sistema de coordenadas rectangulares, entonces la posición estándar de un ángulo se obtiene al colocar el vértice en el origen y hacer que el lado inicial coincida con el $eje x$ positivo. Si el lado inicial $l_1$ se hace girar en dirección contraria al giro de las manecillas de un reloj hasta el lado terminal $l_2$, el ángulo se considera positivo. Mientras que si el lado inicial $l_1$ se hace girar en dirección de las manecillas, el ángulo es negativo.
Se dice que un ángulo $\theta$ está en posición estándar si su vértice está en el origen de un sistema de coordenadas rectangulares y su lado inicial coincide con el lado positivo del eje x.
Medición de ángulos en grados
Una unidad de medida para los ángulos es el grado. La medición de un ángulo en grados se basa en la asignación de 360 grados, se escribe $360°$, al ángulo formado por una rotación completa en sentido contrario al de las manecillas del reloj, como se indica al mover por completo la figura anterior. Entonces, otros ángulos se miden en función de un ángulo de $360°$:
-
- Un ángulo de 1° es el que se forma por $\dfrac{1}{360}$ de vuelta o una rotación completa.
- Un ángulo recto es un ángulo que mide 90°, o $\dfrac{1}{4}$ de vuelta.
- Un ángulo plano $llano$ mide 180°, o $\dfrac{1}{2}$ vuelta.
La siguiente tabla contiene definiciones de otros tipos especiales de ángulos.
| Terminología | Definición | Por Ejemplo |
|---|---|---|
| ángulo agudo $\theta$ | $0^\circ \lt \theta \lt 90^\circ$ | 12° y 39° |
| ángulo obtuso $\theta$ | $90^\circ \lt \theta \lt 180^\circ$ | 93° y 156° |
| ángulos complementarios $\alpha, \beta$ | $\alpha + \beta = 90^\circ$ | 20° y 70°; 8° y 82° |
| ángulos suplementarios $\alpha, \beta$ | $\alpha + \beta = 180^\circ$ | 115° y 65°; 18° y 162° |
La medida en grados para ángulos se emplea en actividades aplicadas como topografía, navegación y el diseño de equipos mecánicos. En aplicaciones científicas que requieren cálculo integral, se acostumbra utilizar medidas en radianes.
Medición de ángulos en radianes
Para definir un ángulo de medida radián, consideremos un círculo de cualquier radio r. Un ángulo central de un círculo es un ángulo cuyo vértice está en el centro del círculo. Si $\beta$ es el ángulo central que se ve en la siguiente figura, decimos que el arco $BC$ denotado $\overline{\rm BC}$ del círculo subtiende a $\beta$ o que $\beta$ está subtendido por $\overline{\rm BC}$.
Si la longitud de $\overline{\rm BC}$ es igual al radio $r$ del círculo, entonces $\beta$ tiene una medida de un radián, como en la siguiente definición.
Definición de radián como medida
Un radián es la medida del ángulo central de un círculo subtendido por un arco igual en longitud al radio del círculo. En radianes se usa la misma convención que con la medida en grados: un ángulo formado por una rotación contraria a las manecillas del reloj se considera positivo, mientras que un ángulo formado por una rotación en el sentido de las manecillas del reloj es negativo.
Si consideramos un círculo de radio $r$, entonces un ángulo $\alpha$ cuya medida es 1 radián interseca un arco $\overline{\rm AP}$ de longitud $r$, como se ilustra en la figura $a$. El ángulo $\beta$ de la figura $b$ mide 2 radianes, porque está subtendido por un arco de longitud $2r$. Del mismo modo, $\gamma$ en $c$ de la figura, mide 3 radianes, porque está subtendido por un arco de longitud $3r$.
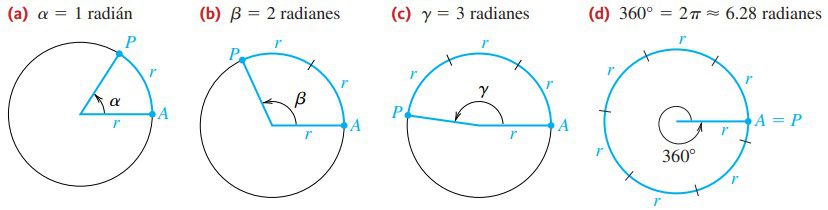
Para hallar la medida en radianes correspondiente a 360°, debemos hallar el número de veces que un arco de circunferencia de longitud $r$ puede trazarse a lo largo de la circunferencia figura $d$. Este número no es un entero y ni siquiera un número racional. Como la circunferencia del círculo es $2 \pi r$, el número de veces que $r$ unidades se pueden trazar es $2 \pi$; por tanto, un ángulo de $2 \pi$ radianes corresponde a 360° y se escribe 360° $360^\circ = 2 \pi \; \text{radianes}$.
Déjanos un comentario No hay comentarios