Una de las piedras angulares de la trigonometría son las “Fórmulas Fundamentales”, un conjunto de relaciones matemáticas esenciales que permiten resolver una amplia variedad de problemas, desde el análisis de trayectorias hasta la determinación de longitudes desconocidas en triángulos.
Fórmula fundamental de la trigonometría
A partir de un triángulo rectángulo de catetos $a, b$ e hipotenusa $c$, el teorema de Pitágoras y la definición dada de las funciones trigonométricas del ángulo $\theta$, se obtiene la fórmula fundamental de la trigonometría.
Partiendo por el teorema de Pitágoras, que establece una relación fundamental entre los lados del triángulo rectángulo: $$a^2 + b^2 = c^2$$ Dividiendo cada lado de la ecuación por $c^2$ se tiene: $$\left$ \frac{a}{c} \right$ ^{2}+\left$ \frac{b}{c} \right$ ^{2} = 1$$
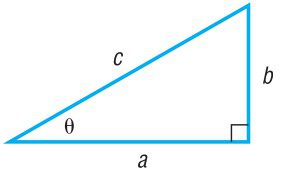
Teniendo en cuenta que $cos\theta = \frac{a}{c}$ y que $sen\theta = \frac{b}{c}$, sustituyendo se obtiene:
$$sen^{2}\theta+cos^{2}\theta=1$$
De esta fórmula se deducen otras identidades trigonométricas:
$$sen^{2}θ = 1 – cos^{2}θㅤㅤyㅤㅤcos^{2}θ = 1 – \text{sen}^{2}θ$$ $$\text{sen}θ = \sqrt{1 – cos^{2}θ}ㅤㅤyㅤㅤcosθ = \sqrt{1 – sen^{2}θ}$$
Demostración
Demostración de la fórmula fundamental de la trigonometría: $\text{sen}^{2}\theta + \cos^{2}\theta = 1 $ Auxiliándonos de la siguiente gráfica:
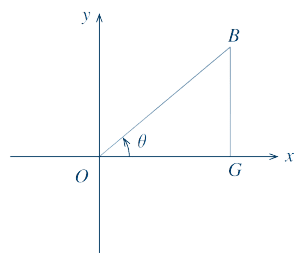
Se tiene que las funciones trigonométricas para el triángulo OGB son: $$senθ=\frac{\overline{\rm BG}}{\overline{\rm OB}}ㅤㅤcosθ=\frac{\overline{\rm OG}}{\overline{\rm OB}}$$ $$tanθ=\frac{\overline{\rm BG}}{\overline{\rm OG}}ㅤㅤcotθ=\frac{\overline{\rm OG}}{\overline{\rm BG}}$$ $$secθ=\frac{\overline{\rm OB}}{\overline{\rm OG}}ㅤㅤcscθ=\frac{\overline{\rm OB}}{\overline{\rm BG}}$$
Al elevar al cuadrado el $\text{sen}θ$ y $\cosθ$, y sumar miembro a miembro se tiene: $$$senθ$^{2}=\left$ \frac{\overline{\rm BG}}{\overline{\rm OB}} \right$^{2}ㅤㅤㅤsen^{2}θ=\frac{\overline{\rm BG^{2}}}{\overline{\rm OB^{2}}}ㅤㅤㅤsen^{2}θ+cos^{2}θ=\frac{\overline{\rm BG^{2}}}{\overline{\rm OB^{2}}}+\frac{\overline{\rm OG^{2}}}{\overline{\rm OB^{2}}}$$ $$$cosθ$^{2}=\left$ \frac{\overline{\rm OG}}{\overline{\rm OB}} \right$^{2}ㅤㅤㅤcos^{2}θ=\frac{\overline{\rm OG^{2}}}{\overline{\rm OB^{2}}}ㅤㅤㅤsen^{2}θ+cos^{2}θ=\frac{\overline{\rm BG^{2}}+\overline{\rm OG^{2}}}{\overline{\rm OB^{2}}}$$
Por el teorema de Pitágoras: $$$HIP$^{2} = $OP$^{2} + $ADY$^{2}$$ Esto es: $$$\overline{\rm OB}$^{2} = $\overline{\rm BG}$^{2} + $\overline{\rm OG}$^{2}$$ Al sustituir tenemos que: $$sen^{2}θ + cos^{2}θ = \frac{\overline{\rm OB^{2}}}{\overline{\rm OB^{2}}}$$ $$sen^{2}θ + cos^{2}θ = 1$$
Identidades principales de Trigonometría
1. Ahora, si dividimos $\text{sen}^{2}θ + \cos^{2}θ = 1$, entre $\cos^{2}θ$, resulta: $$\frac{\text{sen}^{2}θ}{\cos^{2}θ} + \frac{\cos^{2}θ}{\cos^{2}θ} = \frac{1}{\cos^{2}θ}$$ Y al sustituir utilizando fórmulas anteriores como: $$\tanθ = \frac{\text{sen}θ}{\cosθ}ㅤㅤyㅤㅤ\secθ = \frac{1}{\cosθ}$$ Se tiene la siguiente identidad:
$$\tan^{2}θ + 1 = \sec^{2}θ$$
De esta fórmula se deduce que:
$$\tan^{2}θ=\sec^{2}θ-1ㅤㅤyㅤㅤ\sec^{2}θ=\tan^{2}θ+1$$ $$\tanθ=\sqrt{\sec^{2}θ-1}ㅤㅤyㅤㅤ\secθ=\sqrt{\tan^{2}θ+1}$$
2. Si dividimos $\text{sen}^{2}θ+\cos^{2}θ=1$, entre $\text{sen}^{2}θ$, resulta: $$\frac{\text{sen}^{2}θ}{\text{sen}^{2}θ}+\frac{\cos^{2}θ}{\text{sen}^{2}θ} = \frac{1}{\text{sen}^{2}θ}$$ Luego, al sustituir en fórmulas anteriores como: $$\cotθ=\frac{\cosθ}{\text{sen}θ}ㅤㅤyㅤㅤ\cscθ=\frac{1}{\text{sen}θ}$$ Se tiene:
$$1+\cot^{2}θ = \csc^{2}θ$$
De esta fórmula se deduce que:
$$\cot^{2}θ=\csc^{2}θ-1ㅤㅤyㅤㅤ\csc^{2}θ=1+\cot^{2}θ$$ $$\cotθ=\sqrt{\csc^{2}θ-1}ㅤㅤyㅤㅤ\cscθ=\sqrt{1+\cot^{2}θ}$$
Resumen de las funciones
Las fórmulas anteriores se emplean para determinar las funciones de un ángulo cualquiera, cuando se conoce una de ellas.
| sen θ | cos θ | tan θ | cot θ | sec θ | csc θ | |
| sen θ | $\sqrt{1-cos^{2}θ}$ | $\frac{tanθ}{\sqrt{1+tan^{2}θ}}$ | $\frac{1}{\sqrt{1+cot^{2}θ}}$ | $\frac{\sqrt{sec^{2}θ-1}}{secθ}$ | $\frac{1}{cscθ}$ | |
| cos θ | $\sqrt{1-sen^{2}θ}$ | $\frac{1}{\sqrt{1+tan^{2}θ}}$ | $\frac{cotθ}{\sqrt{1+cot^{2}θ}}$ | $\frac{1}{secθ}$ | $\frac{\sqrt{sen^{2}θ-1}}{cscθ}$ | |
| tan θ | $\frac{senθ}{\sqrt{1-sen^{2}θ}}$ | $\frac{\sqrt{1-cos^{2}θ}}{cosθ}$ | $\frac{1}{cotθ}$ | $\sqrt{sec^{2}θ-1}$ | $\frac{1}{\sqrt{csc^{2}θ-1}}$ | |
| cot θ | $\frac{\sqrt{1-sen^{2}θ}}{senθ}$ | $\frac{cosθ}{\sqrt{1-cos^{2}θ}}$ | $\frac{1}{tanθ}$ | $\frac{1}{\sqrt{sec^{2}θ-1}}$ | $\sqrt{csc^{2}θ-1}$ | |
| sec θ | $\frac{1}{\sqrt{1-sen^{2}θ}}$ | $\frac{1}{cosθ}$ | $\sqrt{1+tan^{2}θ}$ | $\frac{\sqrt{1+cot^{2}θ}}{cotθ}$ | $\frac{cscθ}{\sqrt{csc^{2}θ-1}}$ | |
| csc θ | $\frac{1}{senθ}$ | $\frac{1}{\sqrt{1-cos^{2}θ}}$ | $\frac{\sqrt{1+tan^{2}θ}}{tanθ}$ | $\sqrt{1+cot^{2}θ}$ | $\frac{secθ}{\sqrt{sec^{2}θ-1}}$ |
Déjanos un comentario No hay comentarios