Las funciones trigonométricas, pilares fundamentales de la trigonometría, encuentran una poderosa representación en el plano cartesiano. Estas funciones, que describen las relaciones entre los ángulos y las coordenadas de puntos en el plano. Las funciones trigonométricas clave $seno, coseno y tangente$ están relacionadas con estos puntos en el plano, tomando en cuenta la distancia desde el origen $$0, 0$$ hasta el punto dado. Esto crea una conexión directa entre los conceptos geométricos y las funciones matemáticas.
Sistema de coordenadas en el plano
El plano cartesiano consta de dos rectas dirigidas, perpendiculares entre sí llamadas ejes de coordenadas. La recta horizontal recibe el nombre de “$\text{eje }x$” y la recta vertical se le llama “$\text{eje }y$”; el punto donde se intersectan ambas rectas es el origen del sistema.
Cada punto en el plano se describe por un par ordenado $$x, y$$, donde “$x$” representa la coordenada horizontal $$\text{eje }x$$, mientras que “$y$” la coordenada vertical $\text{eje }y$.
En la figura, vemos como los ejes de coordenadas dividen al plano en regiones llamadas cuadrantes. Todo punto $P$ del plano puede localizarse por medio del sistema rectangular; se traza $\overline{PA}$ perpendicular al $\text{eje }x$ y $\overline{PB}$ perpendicular al $\text{eje }y$, la longitud del segmento dirigido $\overline{OA}$ se representa por $x$ y se llama abscisa de P, la longitud del segmento dirigido $\overline{OB}$ se representa por $y$ y se llama ordenada de P. Luego, el punto generado por los números reales $x$ y $y$ se llaman coordenadas de P y se representan como $P$x, y$$.
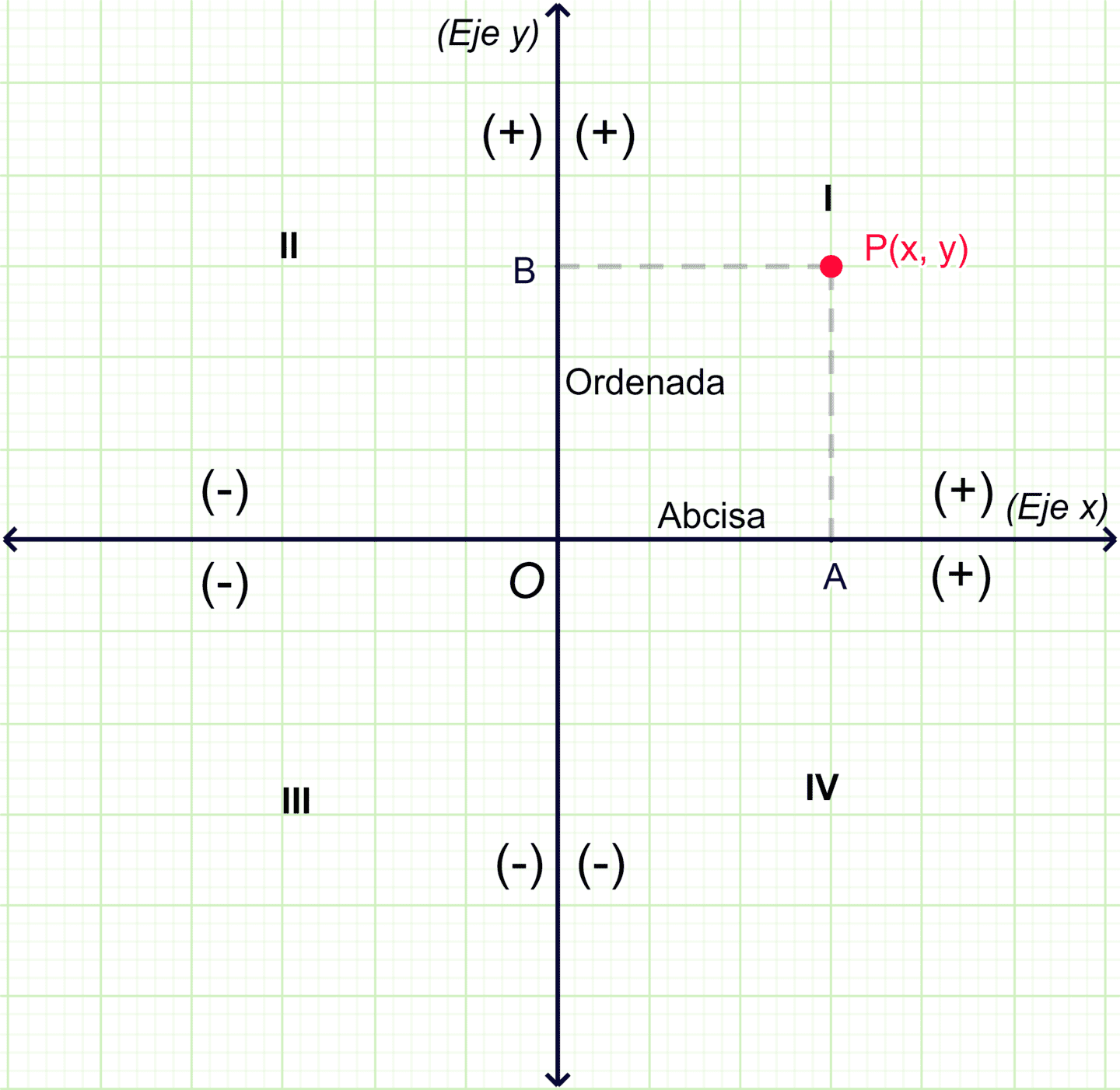
Una referencia para aprender los signos en el plano son las abscisas y las ordenadas, las abscisas medidas sobre el $\text{eje } x$ a la derecha del origen son positivas y a la izquierda del origen son negativas, mientras que las ordenadas que se miden sobre el $\text{eje } y$ son positivas hacia arriba y negativas hacia abajo con respecto al origen.
Ángulo de referencia
Para simplificar el análisis y cálculo de funciones trigonométricas en ángulos fuera del primer cuadrante del plano cartesiano, utilizamos el “ángulo de referencia”. Este es el ángulo agudo formado entre el eje $x$ positivo y la línea que conecta el punto dado en el plano con el origen $0,0$.
Sea $ \theta$ un ángulo en posición estándar tal que su lado terminal no se sitúa sobre un eje de coordenadas. El ángulo de referencia $ \color{#00F}{\theta’}$ para $ \theta$ se define como el ángulo agudo formado por el lado terminal de $ \theta$ y el eje $x$.
La noción del ángulo de referencia es útil para asegurarse de que las funciones trigonométricas tomen el valor correcto en relación con el ángulo original y la ubicación del punto en el plano cartesiano. La siguiente figura ilustra esta definición para los ángulos que tienen lados terminales en cada uno de los cuatro cuadrantes.
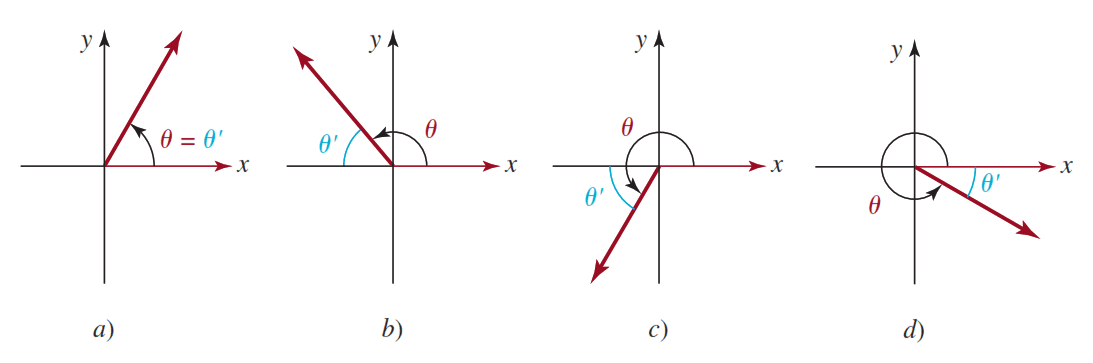
Ejemplos de ángulos de referencia
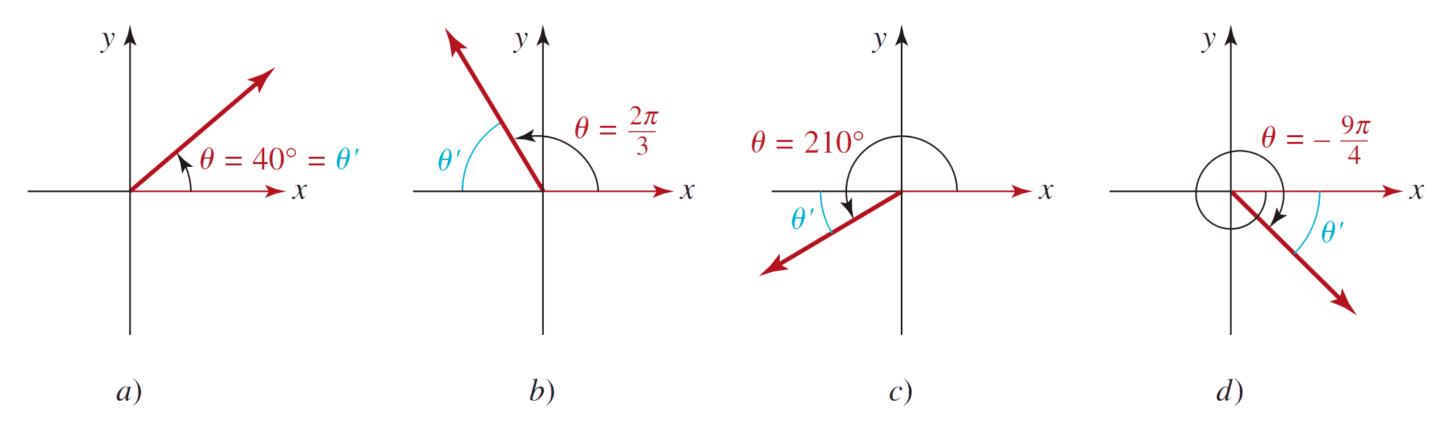
Obtener el ángulo de referencia de cada uno de los cuatro ángulos.
$$\begin{array}{cccc} a$ \; \theta \;=\; 40^\circ \qquad & \qquad b$ \; \theta \;=\; \dfrac{2\pi}{3} \qquad & \qquad c$ \; \theta \;=\; 210^\circ \qquad & \qquad d$ \; \theta \;=\; -\dfrac{9\pi}{4} \end{array}$$
Solución
a$ $\theta \;=\; 40^\circ \text{por definición: } \; \theta \;=\; 40 \;=\; \theta’$
b$ $ \theta’ \;=\; \pi – \theta \;=\; \pi – \dfrac{2\pi}{3} \;=\; \dfrac{\pi}{3}$
c$ $ \theta’ \;=\; \theta – 180^\circ \;=\; 210^\circ – 180^\circ \;=\; 30^\circ $
d$ Puesto que: $ \theta \;=\; -\dfrac{9\pi}{4} $ es coterminal con: $-\dfrac{9\pi}{4} + 2\pi = -\dfrac{\pi}{4} $ Tenemos que $ \theta = \dfrac{\pi}{4}$.
Signos de las funciones trigonométricas
Los signos de los valores de las funciones $\text{sen }t$ y $ \cos t$ quedan determinados por el cuadrante en el que está situado el punto $P$t$$, y viceversa. Por ejemplo, sí $\text{sen }t$ y $\cos t$ son negativos, entonces el punto P$$t$$ y el lado terminal del ángulo correspondiente de $t$ radianes tiene que estar situado en el cuadrante III. En la siguiente tabla se muestran los signos de las funciones trigonométricas y cada uno de los cuatro cuadrantes de los ejes de coordenadas del plano cartesiano:
| Función | Cuadrantes | |||
| I | II | III | IV | |
| Seno | + | + | - | - |
| Coseno | + | - | - | + |
| Tangente | + | - | + | - |
| Cotangente | + | - | + | - |
| Secante | + | - | - | + |
| Cosecante | + | + | - | - |
Déjanos un comentario No hay comentarios