En cálculo y las ciencias es necesario considerar las funciones trigonométricas cuyos dominios están formados por números reales y no por ángulos. Para realizar la transición de ángulos a números reales debemos reconocer que a cada número real $t$ corresponde un ángulo que mide $t$ radianes. Como veremos a continuación, esta correspondencia se puede representar gráficamente con un círculo de radio 1 y centro en el origen en un sistema de coordenadas rectangulares.
Círculo unitario
Se representa gráficamente con un círculo de radio 1 y centro en el origen en un sistema de coordenadas rectangulares. Este círculo se conoce como círculo unitario. La ecuación del círculo unitario es:
$$ x^{2}+y^{2}=1$$
Ahora consideraremos un ángulo central $t$ en posición estándar, es decir, un ángulo cuyo vértice se sitúa en el centro de un círculo y su lado inicial coincide con el $\text{eje }x$ positivo. Según la definición de medida en radianes, el ángulo $t$ se define como $t=\dfrac{s}{r}$, la razón del arco subtendido de longitud $s$ al radio $r$ del círculo. Por el círculo unitario que se muestra en la figura anterior, $r=1$ y, por tanto, $t=s/1$ o $t=s$.
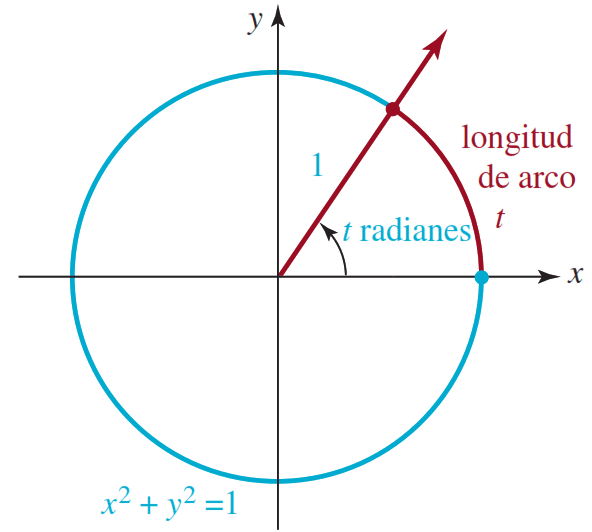
En otras palabras:
En un círculo unitario la medida en radianes de un ángulo de $t$ radianes es igual a la medida $t$ del arco subtendido.
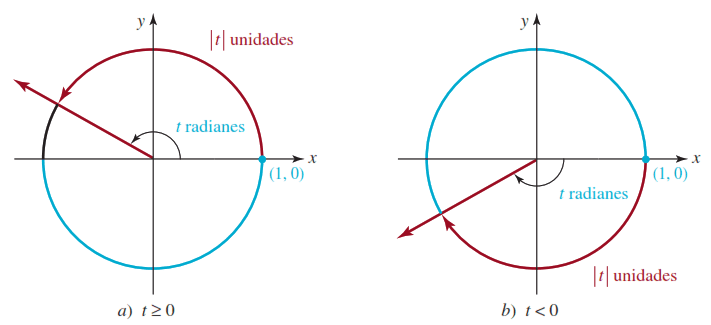
De lo anterior se desprende que para cada número real $t$, el lado terminal de un ángulo de $t$ radianes en posición estándar ha recorrido una distancia de $|t|$ unidades en la circunferencia del círculo unitario: en sentido contrario al de las agujas del reloj si $t>0$ y en el sentido de las agujas del reloj si $t>0$. Esta asociación de cada número real $t$ con un ángulo de $t$ radianes se ilustra en la siguiente figura.
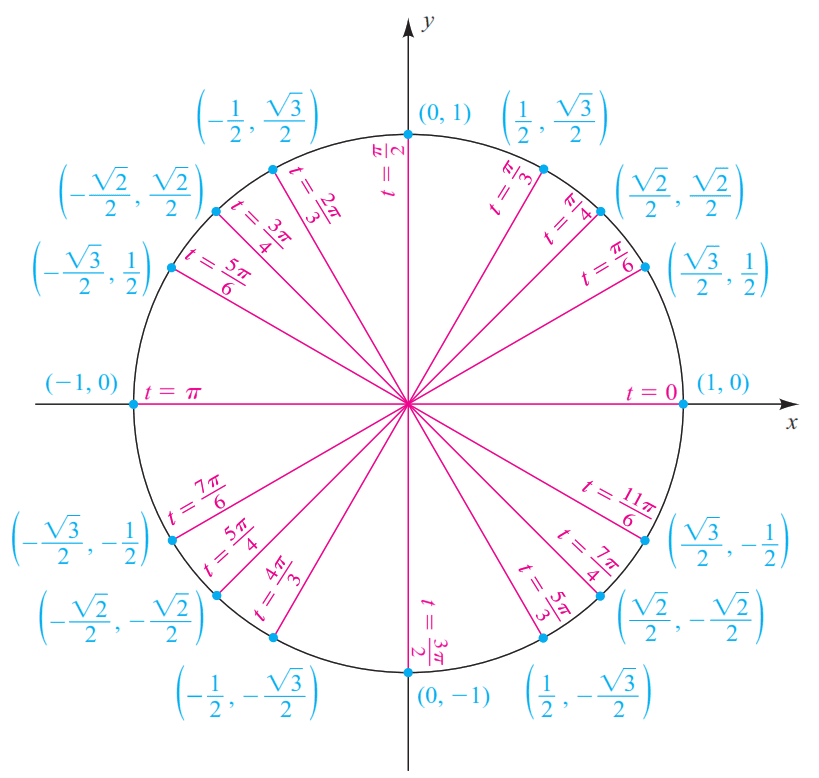
Funciones trigonométricas para ángulos especiales
A continuación se ilustran los valores de las funciones trigonométricas de ángulos especiales en una circunferencia unitaria. Dado el punto $P$x, y$ = P$\cos t, \text{sen}t$$.
Déjanos un comentario No hay comentarios