La Ley del Coseno es una herramienta invaluable en la trigonometría que nos permite resolver triángulos no rectángulos, es decir, aquellos triángulos que no tienen un ángulo recto $90 grados$. Al establecer una relación entre los lados y ángulos, nos capacita para calcular longitudes y ángulos desconocidos con precisión. Con esta unidad pretendemos que puedas entender y aplicar efectivamente la Ley del Coseno; los matemáticos y científicos pueden abordar problemas complejos, aplicados al mundo real, y que involucran triángulos de diferentes formas y tamaños, de ahí que la utilidad de esta Ley en Matemáticas, Ingeniería, Física y muchas otras disciplinas es un testimonio de su importancia en el análisis trigonométrico avanzado.
Los triángulos para los que se conocen tres lados o dos lados y el ángulo incluido $esto es, el ángulo formado por los lados indicados$ no se puede resolver en forma directa usando la ley de los senos. El método que describiremos a continuación se puede usar para resolver triángulos en estos dos casos.
Teorema de Pitágoras
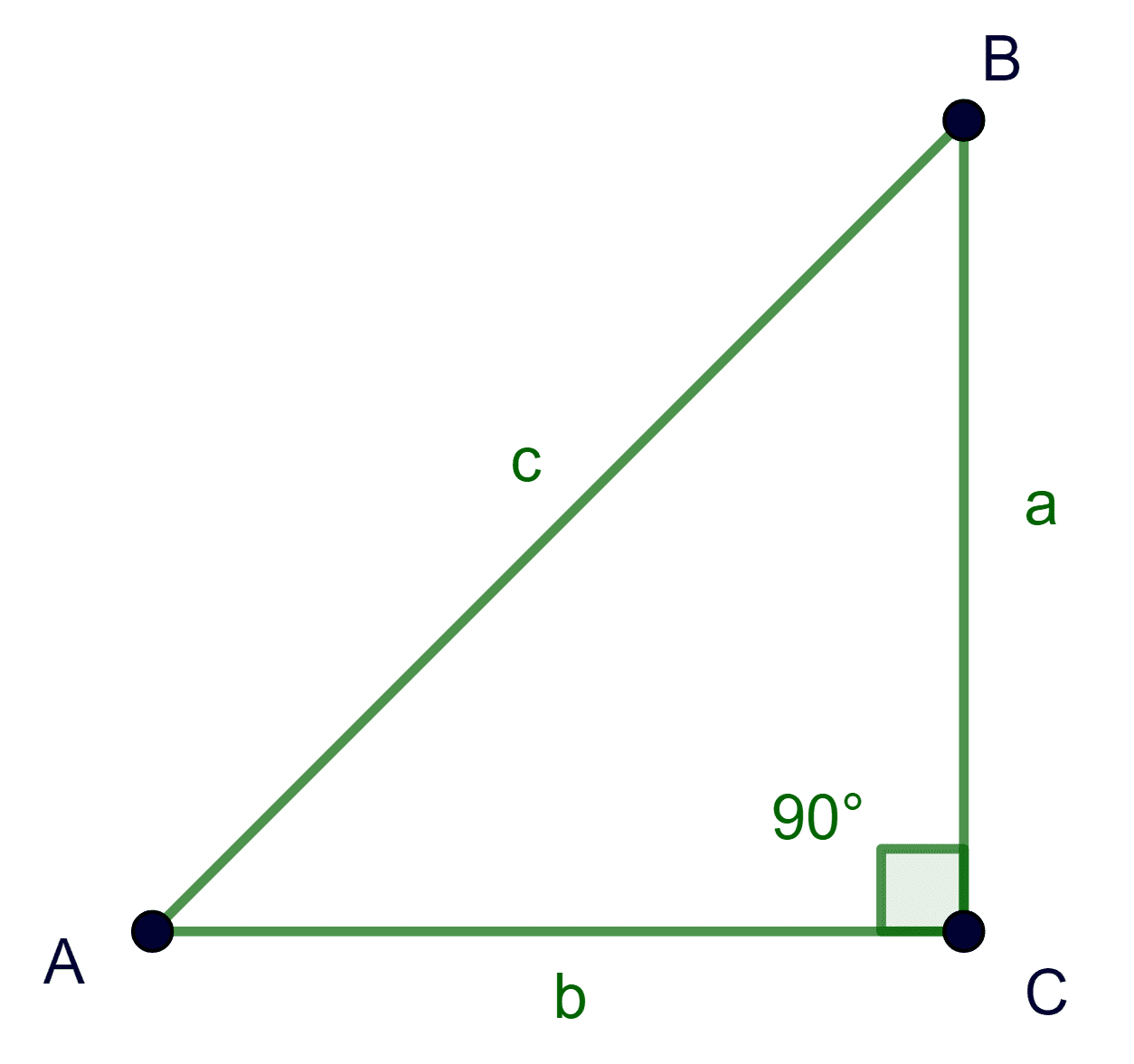
En un triángulo rectángulo, como el de la figura, la longitud $c$ de la hipotenusa se relaciona con las longitudes $a$ y $b$ de los otros dos lados, mediante el teorema de Pitágoras.
$$c^2 = a^2 + b^2 \qquad $1$$$
Esta última ecuación es un caso especial de una fórmula general para relacionar las longitudes de los lados de cualquier triángulo.
Ley de Cosenos
La generalización de la ecuación $1$ se llama ley de los cosenos. Al igual que la ley de los senos de la sección anterior, la ley de los cosenos es válida para cualquier triángulo. La Ley de Cosenos establece una relación entre los lados y ángulos de un triángulo no rectángulo.
En esencia, establece que el cuadrado de la longitud de un lado es igual a la suma de los cuadrados de las longitudes de los otros dos lados, menos el doble del producto de estas longitudes y el coseno del ángulo opuesto al lado que estamos evaluando.
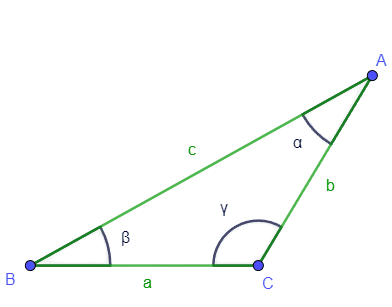
Sean los ángulos $\alpha$, $\beta$ y $\gamma$, y los lados opuestos a ellos sean $a, b$ y $c$, como se ve en la figura. Entonces:
$$\begin{array}{ccc}
a^{2} & = & b^{2} + c^{2} – 2bc \cdot \cos \alpha \\
b^{2} & = & a^{2} + c^{2} – 2ac \cdot \cos \beta \\
c^{2} & = & a^{2} + b^{2} – 2ab \cdot \cos \gamma
\end{array} \qquad \qquad $2$ $$
Se dice que el teorema del coseno $o teorema de los cosenos$ es una generalización del teorema de Pitágoras porque si uno de los ángulos es recto, el triángulo es rectángulo, siendo la hipotenusa el lado opuesto a dicho ángulo y se obtiene el teorema de Pitágoras al aplicar el del coseno.
Por ejemplo, si $ \alpha = 90^\circ$, siendo $ a$ la hipotenusa del triángulo, entonces, la primera de las tres fórmulas anteriores queda como:
$$\begin{align}
a^{2} & = b^{2} + c^{2} – 2bc \cdot \cos$90^\circ$\\
a^{2} & = b^{2} + c^{2} – 2bc \cdot 0\\
a^{2} & = b^{2} + c^{2}\\
\end{align}$$
Demostración del Teorema del coseno
Haremos la demostración por el teorema de Pitágoras $1$. Igual que $1$, la ley de los cosenos es válida para cualquier triángulo. Pero por comodidad deduciremos las dos primeras ecuaciones de $2$ usando el mismo triángulo acutángulo de la figura. Hemos dividido el triángulo $△ABC$ en dos triángulos rectángulos.
Observemos que el lado $\overline{BC}$ es $ c \cos \beta + b \cos \gamma$.
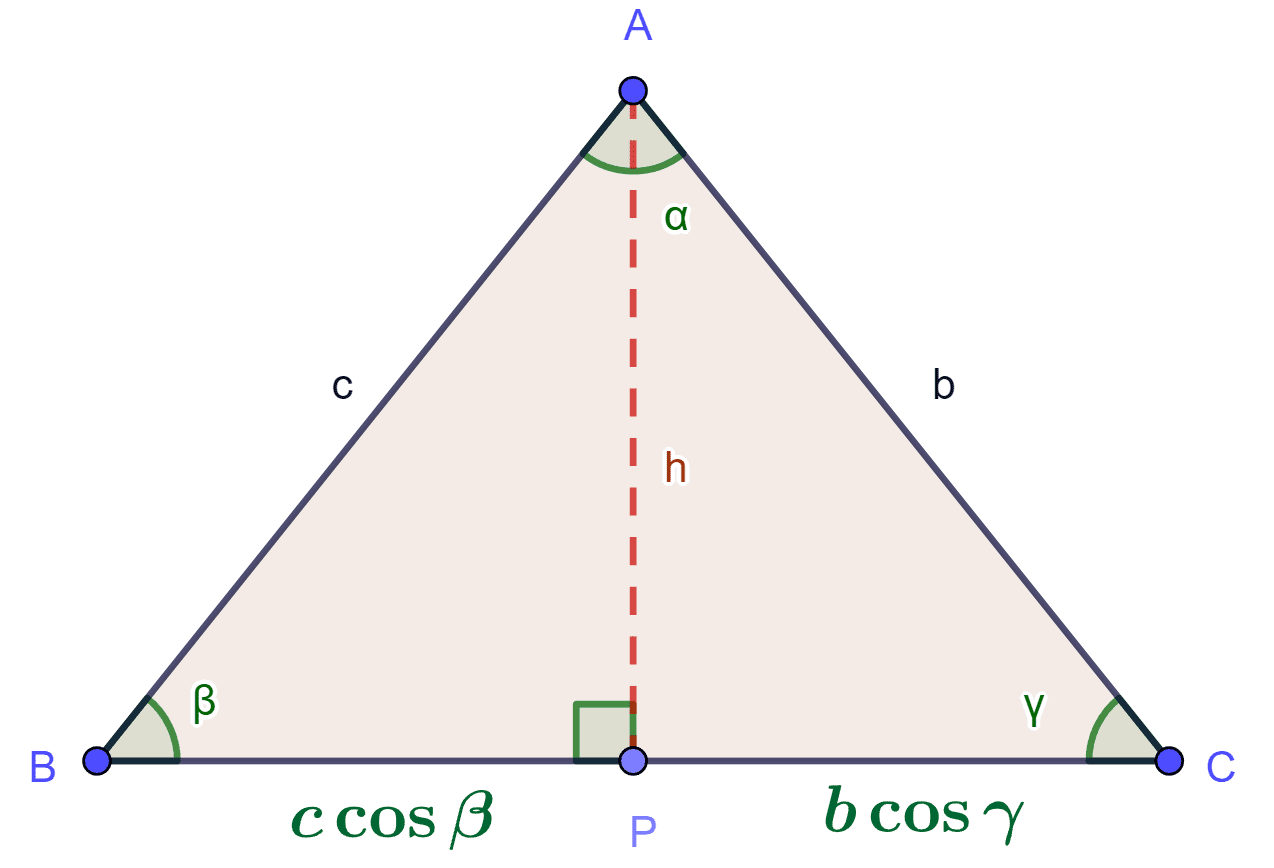
Sin embargo, esta vez sea $P$ el punto donde la altura desde el vértice $A$ cruza al lado $\overline{BC}$. Entonces, como tanto el $△BPA$ y el $△CPA$ de la figura son triángulos rectángulos, de acuerdo con $1$ aplicando el teorema de Pitágoras a estos triángulos, obtenemos las relaciones:
$$\begin{array}{cc}
c^{2} = h^{2}+$c \cos \beta$^{2} & \qquad \qquad $3$ \\
b^{2} = h^{2}+$b \cos \gamma$^{2} & \qquad \qquad $4$
\end{array}$$
Ahora, la longitud de $\overline{BC}$ es $a = c \cos \beta + b \cos \gamma $, por lo que
$$c \cos \beta = a – b \cos \gamma \qquad \qquad $5$$$
Además, por $4$:
$$h^{2} = b^{2} – $b \cos \gamma$^{2} \qquad \qquad $6$$$
Las ecuaciones $5$ y $6$ se sustituyen en $3$, y simplificando la expresión se llega a la tercera de las ecuaciones en $2$:
$$\begin{align}
c^{2} & = b^{2}$b\cos\gamma$^{2} + $a – b \cos \gamma$^{2}\\
c^{2} & = b^{2} – b^{2} \cos^{2}\gamma + a^{2} – 2ab \cdot \cos \gamma + b^{2} \cos^{2}\gamma \\
c^{2} & = a^{2} + b^{2} – 2ab \cdot \cos \gamma \qquad \qquad $7$
\end{align}$$
Déjanos un comentario No hay comentarios