Hace más de 2000 años que la trigonometría fue inventada por los griegos, quienes necesitaban métodos precisos para medir ángulos y lados de triángulos. De hecho, la palabra trigonometría se derivó de dos palabras griegas trigonon triángulo y metria medición.
Este curso inicia con una exposición de los ángulos y cómo se miden, a continuación introducimos las funciones trigonométricas mediante el uso de razones entre lados de un triángulo rectángulo. Luego se dedicará a definir las funciones trigonométricas de los ángulos agudos. Y más adelante, extendemos estas definiciones a los ángulos generales.
Después de extender los dominios de las funciones trigonométricas a ángulos arbitrarios y números reales, consideramos sus gráficas y las técnicas de graficar que hacen uso de amplitudes, periodos y desplazamientos de fase. El curso concluye con una sección sobre problemas de aplicación.
Un poco de historia
Al hablar del origen de la trigonometría estamos también hablando del origen de las matemáticas en general, ya que en un principio todas sus ramas se encontraban íntimamente ligadas. La palabra trigonometría se deriva de dos vocablos griegos: trigon, que significa triángulo, y metro, que significa medida. Por tanto, el nombre trigonometría hace alusión a las diversas relaciones entre los ángulos de un triángulo y sus lados.
De Grecia, la trigonometría pasó a la India y Arabia, donde se utilizaba en astronomía. Desde Arabia pasó a difundirse por Europa, pasando a separarse de la astronomía para ser una rama independiente que forma parte de la matemática.
El astrónomo y matemático griego Hiparco, que vivió en el siglo II antes de Cristo, fue uno de los principales inventores de la trigonometría. Con base en esos fundamentos, Ptolomeo generaliza la relación entre los lados de un triángulo y sus ángulos elaborando unas tablas de funciones trigonométricas, las cuales serán usadas en cálculos astronómicos, se publicó en el primer libro de Almagesto que ha llegado hasta nuestros días. Las tablas de “cuerdas” que elaboró fueron precursoras de las tablas de valores de las funciones trigonométricas que aparecían en todos los textos de trigonometría hasta antes de la invención de la calculadora de mano.
Hiparco $190 - 120 a.C$

El primer matemático europeo que definió las funciones trigonométricas directamente en términos de triángulos rectángulos en lugar de círculos, con tablas de las seis funciones trigonométricas, fue el matemático y astrónomo austriaco Georg Joachim von Lauchen $1514-1574$, también conocido como Georg Joachim Rheticus. Además, Rheticus es recordado porque fue el único discípulo de Nicolás Copérnico $1473-1543$ y el primer defensor de la teoría heliocéntrica del sistema solar propuesta por su maestro.
Más tarde, Isaac Newton $1642-1727$ quien inventó el cálculo diferencial e integral, basando su investigación en la representación de diversas funciones matemáticas empleando series infinitas de potencias de $x$, desarrolló las series para $\sin x$, $\cos x$ y $\tan x$, las cuales son de gran importancia en las matemáticas y sus aplicaciones.
Leonard Euler (Siglo XVIII)

El creador de la trigonometría moderna fue Leonard Euler (Siglo XVIII), quien cimentó el uso de las minúsculas latinas a, b, c, para representar los lados de un triángulo plano o esférico y el de las mayúsculas correspondientes A, B, C para representar los ángulos opuestos a esos lados.
Investigó también las funciones circulares tomando la unidad como el radio de la circunferencia, estas funciones son llamadas las “líneas trigonométricas” y presentadas antiguamente a través de desarrollos de series enteras o en productos infinitos; las cuales forman con las funciones exponenciales y logarítmicas, las funciones trascendentales elementales.
La relación entre las funciones circulares y las funciones exponenciales fueron puestas en evidencia por la genial y audaz intuición de Euler. De este modo, se tiene que, el estudio de las funciones trigonométricas se basa en el estudio general de las funciones.
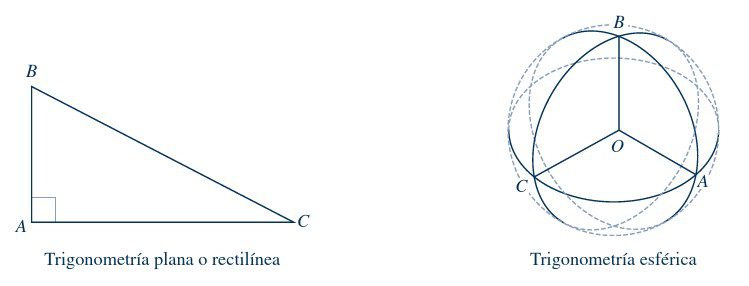
Trigonometría plana
Tiene por objeto el estudio de los triángulos en el plano, sus lados son siempre segmentos de recta, por lo que también se denomina trigonometría rectilínea. En ella, la suma de los tres ángulos interiores de un triángulo es siempre igual a 180°.
Trigonometría esférica
Tiene por objeto el estudio de los triángulos sobre la superficie de la esfera y a toda figura construida sobre ella por arcos de círculos máximos. En ella, la suma de los tres ángulos interiores de un triángulo es siempre mayor que 180° y menor que 360°.
Datos curiosos de la trigonometría
- A comienzos del siglo XVII, el matemático Jhon Napier, fue el que inventó los logaritmos, causantes del empuje que se produjo a los cálculos trigonométricos.
- Newton descubrió la serie para el $\sin x$ y series similares para el $\cos x$ y la $\tan x$.
- La fuente del nombre “seno” proviene la palabra en latín “sinus”, que puede traducirse como “hueco” o “cavidad”, que hacen referencia a la “concavidad” que se genera con un determinado ángulo. Mientras que el término “coseno” puede leerse como una abreviatura de dos palabras, “co” y “seno”; done la primera se refiere a “complemento”, es decir, coseno puede leerse como “complemento del seno”, ya que las funciones seno y coseno difieren, siendo el valor del seno de uno, igual al coseno del otro.
- El matemático Leonhard Euler, el cual en el siglo XVIII demostró que las propiedades de la trigonometría fueron producto de la aritmética de los números complicados, donde consiguió definir las funciones trigonométricas usando expresiones con exponenciales de números complejos.
- Hoy día, es una ciencia indispensable para todos los cultivadores de las ciencias matemáticas. Tanto los ingenieros, los militares y hasta los obreros la usan constantemente como el más preciado de sus auxiliares.
- Su dificultad es solo aparente. Aunque las palabras que ella utiliza se salen del lenguaje vulgar y corriente, es fácil de aprender y aplicar.
Déjanos un comentario No hay comentarios