Los ángulos de 30º, 45º, 60º y 90º son ángulos especiales que se presentan con frecuencia en problemas de aplicaciones matemáticas que se pueden resolver con trigonometría, especialmente donde se encuentran triángulos equiláteros y triángulos rectángulos. De tal forma que, los ángulos agudos de estos triángulos están conformados por ángulos de 45º y otros de 30º y 60º.
Las razones trigonométricas para estos ángulos en función del seno, el coseno y la tangente para los valores de \(x\) más característicos, son las siguientes.
Valores para sen45 y cos45
Para obtener los valores de las funciones seno y coseno de un ángulo de \(45^\circ\), consideramos el triángulo rectángulo isósceles con dos lados iguales de longitud 1 que se ilustra en la figura.
Por la geometría euclidiana sabemos que los ángulos agudos de este triángulo son iguales; por tanto, cada ángulo agudo mide \(45^\circ\). Para obtener la longitud de la hipotenusa, aplicamos el teorema de Pitágoras:
$$(hip)^2 = 1^2 + 1^2 = 2 \quad \text{como resultado,} \quad hip = \sqrt{2} $$
Por definición de las funciones trigonométricas de un ángulo agudo en un triángulo rectángulo, se obtiene:
$$sen 45^\circ = \dfrac{op}{hip} = \dfrac{1}{\sqrt{2}} = \dfrac{\sqrt{2}}{2}$$
$$cos 45^\circ = \dfrac{ady}{hip} = \dfrac{1}{\sqrt{2}} = \dfrac{\sqrt{2}}{2}$$
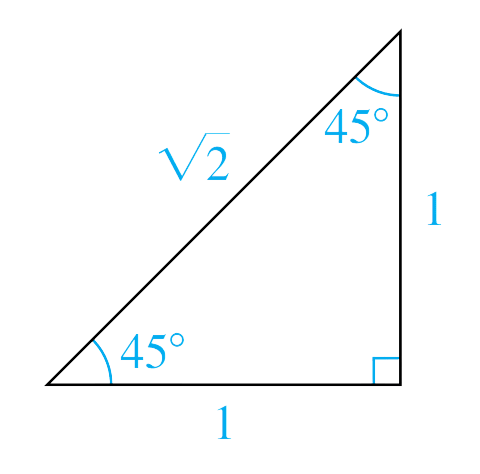
Valores para sen30 y cos30
Para obtener los valores de las funciones trigonométricas de los ángulos de \(30^\circ\) y \(60^\circ\), consideramos el triángulo equilátero \(\text{AOB}\) con lados de longitud 2 que se ilustra en la siguiente figura. Por la geometría euclidiana sabemos que los tres ángulos de un triángulo equilátero miden cada uno \(60^\circ\).
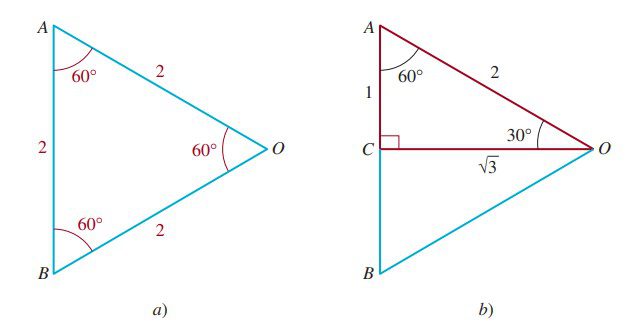
Como se muestra en la figura (b), si dividimos en dos el ángulo en O, entonces \(\text{CO}\) es la bisectriz perpendicular de \(\text{AB}\). Se desprende que:
$$\angle AOC = \dfrac{1}{2}\angle AOB = \dfrac{1}{2}(60^\circ) = 30^\circ $$
$$\overline{\rm AC} = \dfrac{1}{2}\overline{\rm AB} = \dfrac{1}{2}(2) = 1 \Longrightarrow \angle ACO = 90^\circ$$
Si aplicamos el teorema de Pitágoras al triángulo rectángulo rojo ACO de la figura anterior, obtenemos \( (\overline{\rm CO})^2 + 1^2 = 2^2 \). Despejamos \( \overline{\rm CO} \) y obtenemos \( \overline{\rm CO} = \sqrt{3} \). Por tanto, del triángulo rectángulo \(\text{ACO}\) y de las funciones trigonométricas de un ángulo agudo en un triángulo rectángulo, obtenemos los siguientes valores:
$$\sin 30^\circ = \dfrac{op}{hip} = \dfrac{1}{2}$$
$$\cos 30^\circ = \dfrac{ady}{hip} = \dfrac{\sqrt{3}}{2}$$
Valores para sen60 y cos60
Ahora usamos el ángulo de \(60^\circ\) del triángulo rectángulo rojo \(\text{ACO}\) de la figura anterior (b) e identificamos \( op = \sqrt{3}, ady = 1\) e \( hip = 2 \). Por tanto:
$$sen 60^\circ = \dfrac{op}{hip} = \dfrac{\sqrt{3}}{2}$$
$$cos 60^\circ = \dfrac{ady}{hip} = \dfrac{1}{2}$$
Ejemplo
Encuentre los valores de las funciones trigonométricas de \(30^\circ\), \(45^\circ\) y \(60^\circ\) que corresponden a \(\phi\):
$$\begin{array}{ccc} a)\; \phi = 60^\circ & b)\: \phi = 30^\circ & c) \phi = 45^\circ \end{array}$$
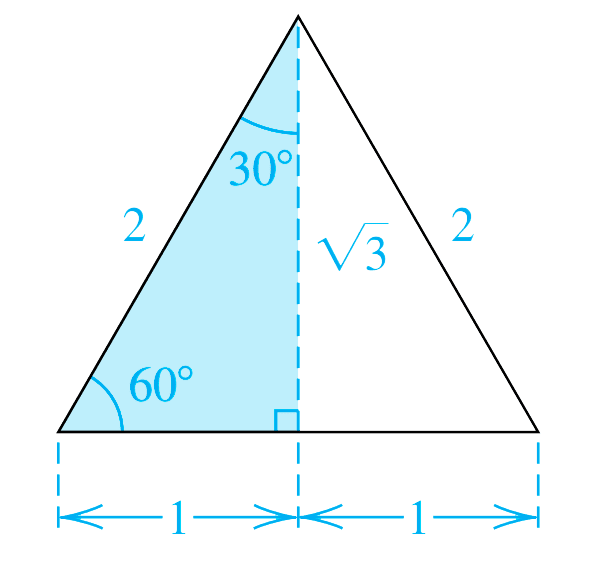
Solución. Considere un triángulo equilátero con lados de longitud 2. La mediana de un vértice al lado opuesto biseca el ángulo en ese vértice, como se ilustra con una línea interrumpida en la figura.
Por el teorema de Pitágoras, el lado opuesto a \(60^\circ\) en el triángulo rectángulo sombreado tiene longitud \(\sqrt{3}\). Usando las fórmulas para las funciones trigonométricas de un ángulo agudo de un triángulo rectángulo, obtenemos los valores correspondientes a \(60^\circ\) y a \(30^\circ\) como sigue:
(a) Para los valores de \( \phi = 60^\circ \):
$$\begin{array}{lll} sen 60^\circ = \dfrac{\sqrt{3}}{2} & \cos 60^\circ = \dfrac{1}{2} & \tan 60^\circ = \dfrac{\sqrt{3}}{1} = \sqrt{3} \\ \csc 60^\circ = \dfrac{2}{\sqrt{3}} = \dfrac{2\sqrt{3}}{3} & \sec 60^\circ = \dfrac{2}{1} = 2 & \cot 60^\circ = \dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{3}}{3} \end{array}$$
(b) Para los valores de \( \phi = 30^\circ \):
$$\begin{array}{lll} sen 30^\circ = \dfrac{1}{2} & \cos 30^\circ = \dfrac{\sqrt{3}}{2} & \tan 30^\circ = \dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{3}}{3} \\ \csc 30^\circ = \dfrac{2}{1} = 2 & \sec 30^\circ = \dfrac{2}{\sqrt{3}} = \dfrac{2\sqrt{3}}{3} & \cot 30^\circ = \dfrac{\sqrt{3}}{1} = \sqrt{3} \end{array}$$
(c) Para los valores de \( \phi = 45^\circ \), podemos considerar un triángulo rectángulo isósceles cuyos dos lados iguales tienen longitud 1, como se ve en la figura. Por el teorema de Pitágoras, la longitud de la hipotenusa es \( \sqrt{2} \) y, por tanto, los valores correspondientes para \(45^\circ\) son:
$$\begin{array}{ll} sen 45^\circ = \dfrac{1}{\sqrt{2}} = \dfrac{\sqrt{2}}{2} = \cos 45^\circ & \tan 45^\circ = \dfrac{1}{1} = 1 \\ \csc 45^\circ = \dfrac{\sqrt{2}}{1} = \sqrt{2} = \sec 45^\circ & \cot 45^\circ = \dfrac{1}{1} = 1 \end{array}$$
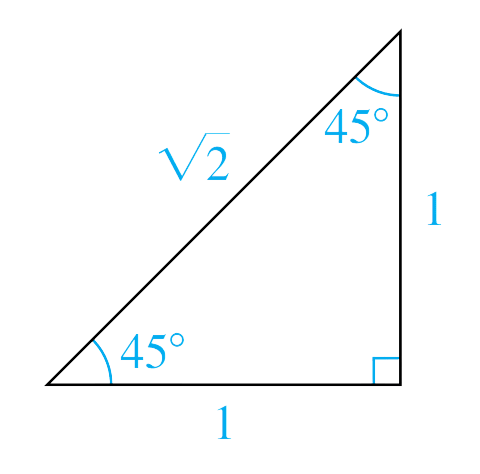
Tabla de valores numéricos de las funciones trigonométricas
Es importante estudiar los valores numéricos de las funciones trigonométricas para los ángulos de \(30^\circ\), \(45^\circ\) y \(60^\circ\). Puesto que podrán ser implementados, frecuentemente, para resolver problemas de aplicación al mundo real.
| Ángulo | sen | cos | tan | cot | sec | csc |
| $$30^\circ$$ | $$\frac{1}{2}$$ | $$\frac{\sqrt 3}{2}$$ | $$\frac{\sqrt 3}{3}$$ | $$\sqrt 3$$ | $$\frac{2 \sqrt 3}{3}$$ | $$2$$ |
| $$45^\circ$$ | $$\frac{\sqrt 2}{2}$$ | $$\frac{\sqrt 2}{2}$$ | $$1$$ | $$1$$ | $$\sqrt 2$$ | $$\sqrt 2$$ |
| $$60^\circ$$ | $$\frac{\sqrt 3}{2}$$ | $$\frac{1}{2}$$ | $$\sqrt 3$$ | $$\frac{\sqrt 3}{3}$$ | $$2$$ | $$\frac{2 \sqrt 3}{3}$$ |













